A question that comes up from students from time to time is why we discourage secondary references in literature reviews, and it struck me that this is not just a one-dimensional question with a simple answer, but it actually leads to a rather interesting process which I have chosen to call literature review forensics. Forensics is defined as ‘relating to or denoting the application of scientific methods and techniques to the investigation of crime.’ Oh wait, was this a primary reference? Possibly not – it was the first definition that came up in a Google search. Best try a little harder. I checked the Oxford Dictionary. Same definition (phew!). Seems a bit strong, you might think, to associate crimes with literature reviews. Perhaps you will allow the working definition of ‘relating to or denoting the application of scientific methods and techniques to the investigation of secondary referencing’.
The problem of secondary referencing is that sources are apparently so easy to find these days (so much easier than when I started my PhD, trying to find printed journals in the library, waiting weeks for photocopied articles to arrive in the post through interlibrary loan), yet their real origin is sometimes less evident. An example of this in teaching and learning is the poster-like quotes that litter the Web from various supposed sources. A common example is “education is not the filling of a bucket (or pail) but the lighting of a fire”. Do an image search for that on Google and you will get an avalanche of hits. There must be thousands of these on classroom walls. The quote is variously attributed to W.B. Yeats, Socrates, Churchill etc. but in fact appears to come from an original quote by Plutarch as stated by David Boles. Oh wait, I have fallen into my own trap by quoting an unrefereed blog post. Well, more of that later.
Here’s another one you might have come across, supposedly from John Dewey; “If we teach today’s students as we taught yesterday’s, we rob them of tomorrow”. Awesome quote but I don’t think Dewey ever said it, or perhaps he said it but didn’t write it down. I take some corroboration from this blog post by Tryggvi Thayer. You’re probably thinking that once again I have fallen into the trap of citing another secondary reference, but in this case I did my very best to try to find the quote, since Dewey’s books are now out of copyright and available on the Web. I did an extensive search (up to the point where I lost the will to live, anyway) and was unable to find anything resembling that quote, so I’m fairly confident it doesn’t really exist. The fact that one of Dewey’s books was called ‘Schools of To-morrow‘ (with a hyphen) suggests an example of what I mean by forensics, looking a little bit deeper into the evidence before making assumptions about sources. One might assume that the book contains the quote by virtue of its title. Rookie mistake.
The first issue with secondary references is, of course, that your primary reference may be interpreting the other writer in a way that you do not think is reasonable. In fact they may just be making it up. You have no way of knowing unless you check the original reference, and this is often where you disappear into a rabbit hole, because the primary reference has taken a secondary reference from another source which was also using the second secondary reference and so on ad infinitum until either you can find the original reference or, as in some cases, it turns out be impossible.
A couple of examples I have come across are the following two diagrams, both supposedly sourced diagrams about enquiry learning. You might think it’s unreasonable to treat diagrams as references, but they still need to have their sources properly acknowledged, and if they claim to represent someone else’s ideas, do they really?
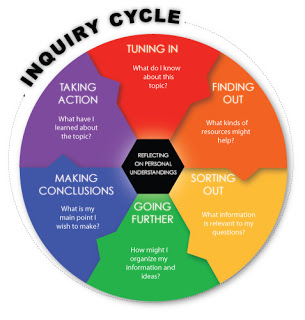

In the first example, ‘Murdoch’s Inquiry Cycle’, the academic source probably exists – it seems to be an amalgam of work from Murdoch, Branch, Stripling and Oburgbut – but it seems unlikely that this specific image came from any of those articles (please correct me if I’m wrong). There are many variations on the Web, none properly referenced as far as I can see. The second example, ‘Brunner’s Inquiry Process Model’, supposedly comes from a 2002 source, but I can’t find any evidence of the original version whatsoever. You could try starting at the University of Cambridge and see if you have more success than me. Of course these images (or their precursors) come from someone, and it may be that there is a proper reference hiding out there somewhere. My point is that it is sometimes really hard to find. That’s why my two example links come from blog posts by authors who clearly have no idea of the source of their material.
I think what these examples show is that it is a worthwhile and quite fascinating skill for students to develop a forensic approach to the literature. Ideally of course this would all be supported by a tool. The nearest one I can think of is Turnitin. Unfortunately, because Turnitin is primarily oriented towards detecting plagiarism rather than easily showing you the original source, it is much keener on showing you that your work is duplicating the work of some other student, rather than finding which mutual source was originally used, and it does take some manual delving around to try to gain any of this information from the Turnitin interface. It would be great if someone could develop a tool that could do literature review forensics and cut through the repetitions of mis-quotes, inventions and distortions that multiply endlessly and mislead the unwary researcher.
So, anyway, what about that Plutarch quote? Well, the blog I mentioned earlier links to a Google Books site suggesting that the source appears in Plutarch’s ‘Essays’ but unfortunately I was unable to find it, nor in Plutarch’s ‘Morals’. I’m not saying it isn’t there, just that a Google search of the text file to find anything resembling that quote failed miserably. Perhaps W.B. Yeats wrote that after all?
As a final note, one supposed quote that was widely circulated following the death of Stephen Hawking was the following; “The greatest enemy of knowledge is not ignorance, it is the illusion of knowledge.” Once again, this does not appear to be an authentic quote from Hawking, but nevertheless beautifully sums up the dictum that we should always know where our supposed knowledge comes from.

How does the application of scientific methods and techniques come into play in literature review forensics?